How to Read a Pump Curve

How to read a pump Curve

Pumps are often considered as a machine which will provide a required flow and pressure, however in reality the performance of a pump is dictated by a performance curve detailing how the pump will provide a range of flows at differing pressures.

Pumps provide a differential pressure and flow according to their installation. As there are 3 main families of pumps being Centrifugal, Rotary Positive Displacement and Reciprocating Positive Displacement which have different characteristics dependent on the circumstances they face.

What is a pump performance curve?

Pumps are a simple machine which provide a performance based on the system it works in, as most pumps do not have a control interface unless fitted with a pressure transducer and variable frequency drive (VFD) and must be manually commissioned onsite.

A pumps performance will be inline with the pressure losses in the system, with pumps producing a differential flow and pressure based on the conditions at the inlet. A pump curve is a graphical representation of what flows and differential pressures can be produced by a pump.

As 90% of problems with pumps are caused by the system they are installed in, it is important to note that pump selection is just part of the process of selecting a pump which is right for the process.

In order for a pump to be selected for your process it is important that the following are known:
1. Fluid being pumped
2. Application
3. Flow Required
4. Pressure required
5. Viscosity of fluid & Specific Gravity
6. Temperature
7. Power available / Power medium being used to drive pump.

There are two types of pump curves dependent on the pump selected, which are Centrifugal Pumps and Positive displacement Pump Curves.

Centrifugal Pump Curve 

Centrifugal pumps account for 70% of pumping applications, and their curves are generally shaped with a half moon shape with the highest point on the left showing highest pressure but lowest flow, and the far right end of curve showing highest flow but lowest amount of pressure. The duty point is is marked typically with the efficiency indicated in percent.

The numbers at the end of the curve is the impeller diameter, which is trimmed to acheive the required flow and pressure. The more an impeller is trimmed the higher the impact on a pumps efficiency as the gap between the outside of the impeller and casing is larger creating inefficiencies.

Although a pump curve shows the various duty points that a pump can achieve, operating the pump in some of the areas of operation can lead to many problems.  

Best Efficiency Point (BEP)

As you can see in the illustration across and above pump curve there is a point typically midway curve known as the Best Efficiency Point which is the most efficient point at which the pump can be operated at.

As you can see in the below illustration if the pump is operated on the left it can mean low bearing life, mechanical seal failure and heavy vibration.

If a pump is operated too far left on its curve there is no allowance for extra capacity should there be miscalculation in system pressures. Too far to the right and there is the risk of cavitation which can destroy the pump casing and impeller very quickly and cause the liquid to boil. Good practice is to always have a safety margin maybe 10% towards the left of the duty point to ensure the pump can operate as required, as a pumps performance can always be reduced, but not increased.

Positive Displacement Pump Curve

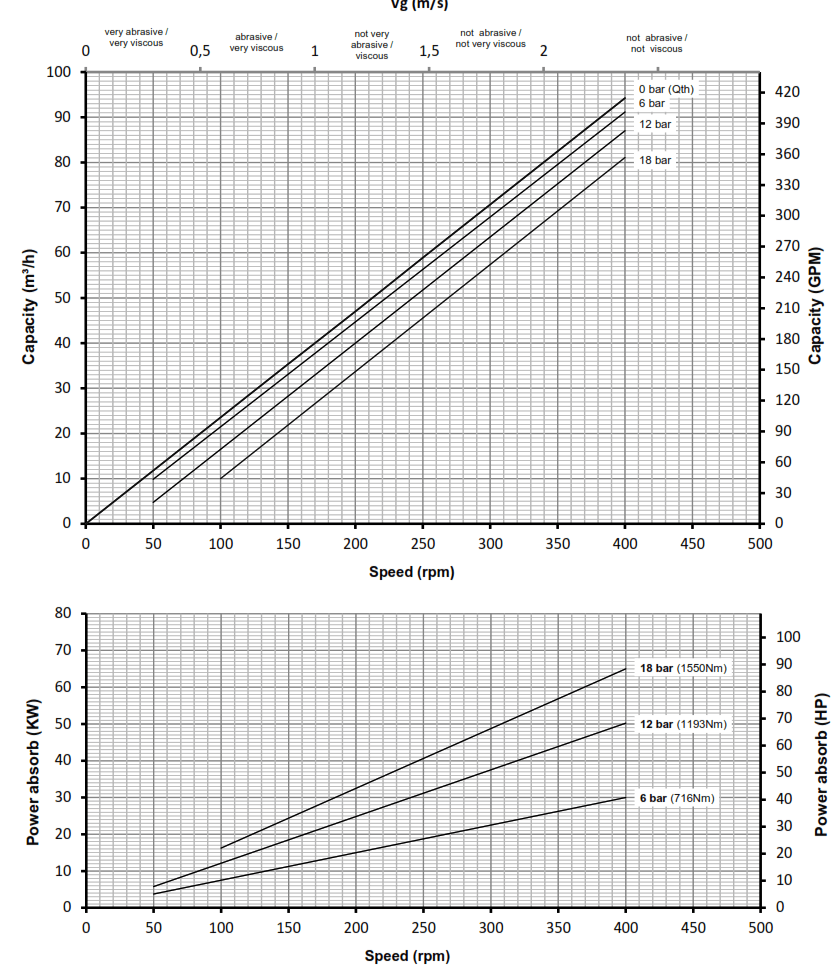
A positive displacement curve is different to that of a centrifugal pump curve as it is usually a straight line. 

This is because a positive displacement pump flow is proportional to rpm and does not decrease with pressure like a centrifugal pump. A PD pump curve usually has a separate axis detailing viscosity, where the pump will show a flow against viscosity as per the graph below.

What is a NPSH Pump Curve?

The NPSH pump curve shows the Net Positive Suction Pressure Required (NPSH) in Metres (M) to deliver the duty point. The NPSH of a centrifugal pump is typically stable on the left side of the axis, where a pump is producing the highest pressure but lowest flow. After the Best Efficiency Point the NPSH curve steadily increases before rising sharply at the end of the performance curve where the pump will cavitate if operated. The NPSH curve is more relevant to rotary centrifugal pumps and less relevant to positive displacement pumps which are less likely to operate end of curve and cavitate. In the below curve an NPSH of 3.32M is required to deliver the required performance. 

What is a system curve?

A system curve provides a graphical image of the pump head required to move fluid around the designed system. The system curve considers the losses of all the required components at various flows  within the system, as well as the static head. A system curve will be plotted on to a pump curve, and where the two intersect determines the flow and pressure which will be produced in the system.

What is a pump efficiency curve?

A pump efficiency curve shows the efficiency of a pump across the range of flows and pressures produced by a pump. On the left hand side of the curve the efficiency will range from 0 to a maximum of around 85% efficiency before decreasing after approximately mid performance curve. Ideally a pump should be operated as close as possible to its BEP for maximum component life, and minimal wear.

Outside of the Best Efficiency Point (BEP) the pumps performance will suffer and if operated inefficiently can damage itself, leading to its destruction within minutes.

Pump curve vs rpm

Pump curves are shown at full motor speed, but if the speed of the pump is reduced the curve will reduce. The outer edge of the curve will step inwards towards the axis on all sides meaning a reduction in both outlet pressure and flow. Reducing a pumps speed is more efficient than reducing an impeller diameter as the clearances between the impeller tip and casing remain small. 2 pumps operating at 50% capacity will save more energy than one pump operating at full capacity.

Pump curve vs power

The power a pump uses to deliver a specific performance varies according to where the pump operates on its curve. Pumps are often fitted with larger motors than required for the duty point, to ensure should the pump operate towards the end of its curve it will continue to operate as required and not trip. As you can see in the below curve on the far left the pump absorbs (uses) just over 3.5Kw, and at duty point to deliver the flow required a power of 7.09kw is required. The power absorbed by the pump continues to rise after the duty point, meaning in practice a pump should be fitted with a motor of at least 7.5kw to cover end of pump curve.

Important Notes & Assumptions

Curve Basis
Curves are always based on fresh water at 20°C at sea level which may not reflect the requirements of your application which is why the fluid viscosity and specific gravity are required to create an accurate representation of what your equipment will achieve.

Viscosity
Viscosity can vary significant with certain fluids such as oils and it is important to ensure the figure quoted is correct. Many fluids have a viscosity quoted at 20°C or 60°C which can be far from the actual pumping temperature especially in cooling applications where the pump is required to work prior to the oil being heated.

Minimum Continuous Safe Flow (MCSF)

The Minimum Continuous Safe Flow is the minimum amount of a flow a centrifugal pump can do without sustaining issues such as cavitation, or excess wear and is often a figure used to design operating speeds, and bypass control valves in processes where pumps may be running continuously such as boiler feed applications, cooling or in lubrication applications.

Motor Pole sizes

Motors on centrifugal pumps revolutions are set by the number of poles in the motor. The more poles a motor has the slower it will operate at. Increasing the number of poles in a motor can help pumps to produce more flow at lower pressures, and gain from a reduction in the NPSH required, suffer from less wear and tear, and utilize a smaller powered motor. If a higher pressure is required and lower flow pumps will operate at higher RPM to generate the pressures required.

Changing the number of poles in motor is not the only way to change pump speed. Pumps can also be set at individual rpms if used through an inverter or mechanical variator. Positive displacement pumps will usually use a gearbox with a pump operating at full motor speed in order to ensure the pump operates at a set RPM.

Some applications will require a pump to operate for a short amount of time, and others for 24/7 such as in cooling at which point a low motor speed will be chosen. A PD pump may have a 2 pole motor rather than a higher pole due to the starting torque. Care should also be taken as motors can be listed as having a high RPM but in actual fact the rpm may be rated as less from the motor. North Ridge Pump curves are specified to the exact RPM of the motor rather than using a general figure.

Pump Design Tolerances - ISO9906 Testing

ISO9906:2010 details the hydraulic performance criteria a rotodynamic pump must adhere to. There are three levels of acceptance being:

·         1B, 1E and 1U

·         2B and 2U

·         3B

This means that depending on the class used for testing the head can vary between +- 0% to +-7% and flow between 0% to +-9% which requires careful consideration during pump selection. This is often why margins are added to requested performance.

Table of Pump Design Tolerances

Pump curve affinity law

The pump affinity laws are a set of formula which can be used to determine a pumps performance when a change is made such as speed, or impeller diameter to the produced flow and pressure with a high degree of accuracy.

There are 3 affinity laws:

1) Flow is proportional to the shaft speed or impeller diameter

As the shaft speed or the impeller diameter is altered, the flow will change by the same amount. If the speed of a pump is reduced by 20% the flow at the same head will also decrease by 20%.

2) The pressure produced is proportional to the square of shaft speed or impeller diameter

When the impeller diameter is altered or shaft speed is changed pressure changes proportional to the square of the change in shaft speed or impeller diameter. If a shafts speed increases by 10% then pressure at the same flow will increase by 21%

3) Power is proportional to the cube of shaft speed or impeller diameter

If the shaft speed increases by 10%, then due to power being proportional to the cube of shaft speed the power will increase by 33.3%.